
В данной работе представлена разработанная авторами прикладная теория локального контактного взаимодействия упругих тел и создание на ее основе процессов формообразования опор трения-качения с рациональной геометрией, направленной на повышение работоспособности подшипниковых узлов различных механизмов и машин.
Весьма важным направлением в повышении качества опор трения качения является технологическое обеспечение рациональной геометрической формы их рабочих поверхностей: тел и дорожек качения. В работах В.М. Александрова, А.В. Королева [1], А.И. Лурье, А.В. Орлова, И.Я. Штаермана [2] и др. убедительно показано, что придание рабочим поверхностям упруго контактирующих деталей механизмов и машин рациональной геометрической формы позволяет существенно улучшить параметры упругого контакта и значительно повысить эксплуатационные свойства узлов трения.
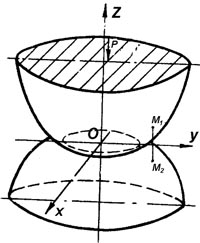
Как известно, впервые решение контактной задачи для случая гладких тел с начальным
одноточечным контактом было дано Герцем в конце XIX века. При решении Герц
рассматривал контактирующие тела, начальный зазор которых описывался уравнением
z1 - z2= A·x2+B·y2,
т.е.
для тел, имеющих круговой профиль вдоль главных осей, что никак не учитывала форму контактирующих тел, от которой и завит этот первоначальный зазор.
При контакте поверхностей сложной формы начальный зазор можно описать уравнением:
z1 - z2= A·xm+B·yn,
где показатели степени как раз и учитывают форму тел вдоль главных осей деталей.
Нами была решена данная задача [3], [4], [5]. Теперь появилась возможность рассчитывать все характеристики контакта в зависимости от формы тел. И наоборот, подбирая необходимые характеристики контакта задавать необходимую для этого форму тел.
Полученные нами выражения, при n = m = 2 вырождались в формулу Герца, а при n = m = 4 в выражение, полученные Штаерманом И.Я.
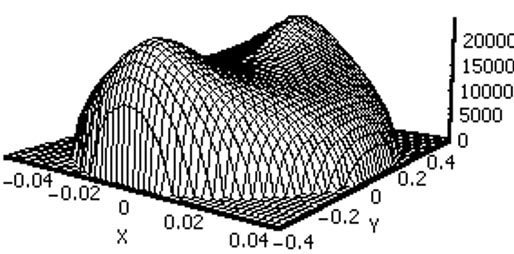
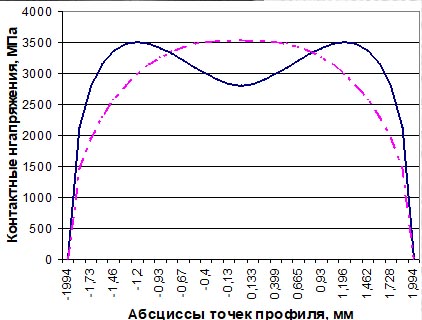
Ниже на рисунке представлен эпюр контактных напряжений, получаемой из теории Герца (слева) и для тел, начальный зазор которых описывается при m = 2, n = 6

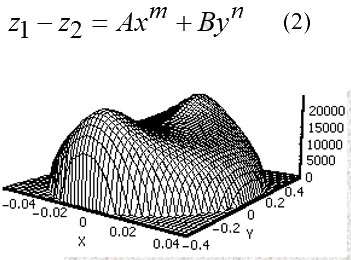
Из рисунков видно, что для круговых тел (формулы Герца), максимальное контактное напряжение достигается в центре площадки контакта, где в случае опор трения качения возникает максимальное микропроскальзование (например, для шариков по стандартной дорожке качения), а, следовательно, и происходит максимальный износ подшипников.
Если же поперечный профиль дорожки качения изменить так, что бы начальный зазор вдоль поперечной оси описывался бы степенной функцией 6 степени (например, таким образом изменить, поперечный профиль дорожки качения подшипников), то как видно из рисунка, в центре площадки контакта напряжения значительно уменьшаются, а учитывая, что именно здесь происходит максимальное микропроскальзование, то существенно уменьшается и износ контактирующих тел. Кроме того, максимальные напряжения, возникающие в других точках контакта, в 2 раза меньше, чем на стандартном профиле, что также существенно влияет на долговечность и работоспособность подшипников.
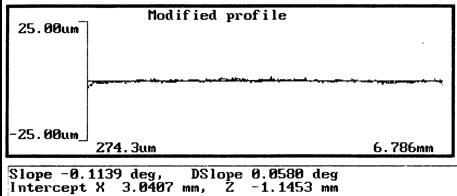
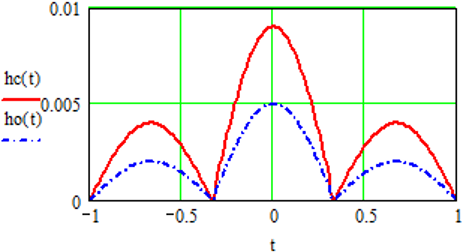
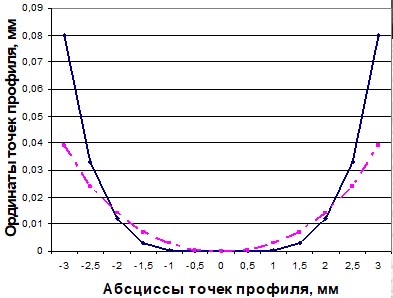
Ниже показаны сравнительные графики стандартного профиля (рассчитанных по формулам Герца) и профиля для m = 2, n = 6:
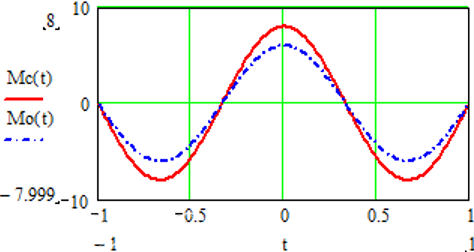
--- Оптимизимрованный профиль
--- Оптимизимрованный профиль
--- Оптимизимрованный профиль
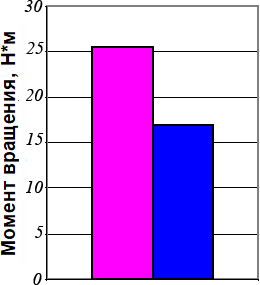
Как видно из графиков, при оптимизированном профиле дорожке качения снижаются момент трения в центре площадки контакта, существенно снижается износ, а также момент вращения подшипников.
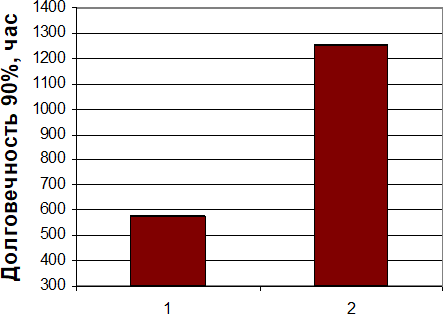
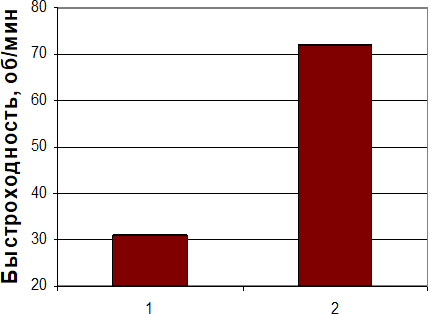
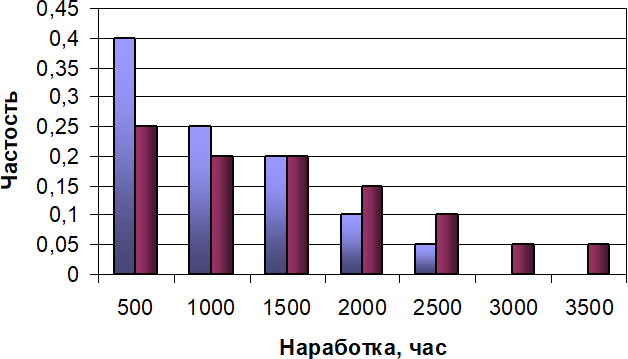
Ниже показаны результты стендовых испытаний подшипников, проводимых на базе ОАО "Саратовский подшипниковый завод".
-


--- Оптимизимрованный профиль
--- Оптимизимрованный профиль
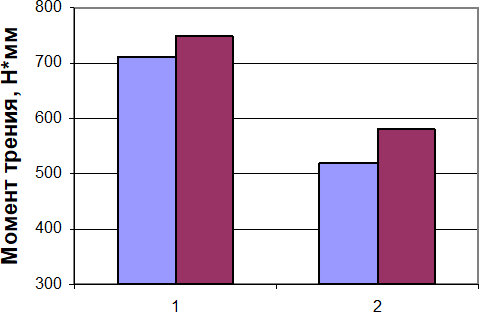
--- Оптимизимрованный профиль
1 - тороидальный профиль; 2- парабола 6-й степени